My favourite curve

So what is your favourite curve (do you even have a favourite curve? You should!)

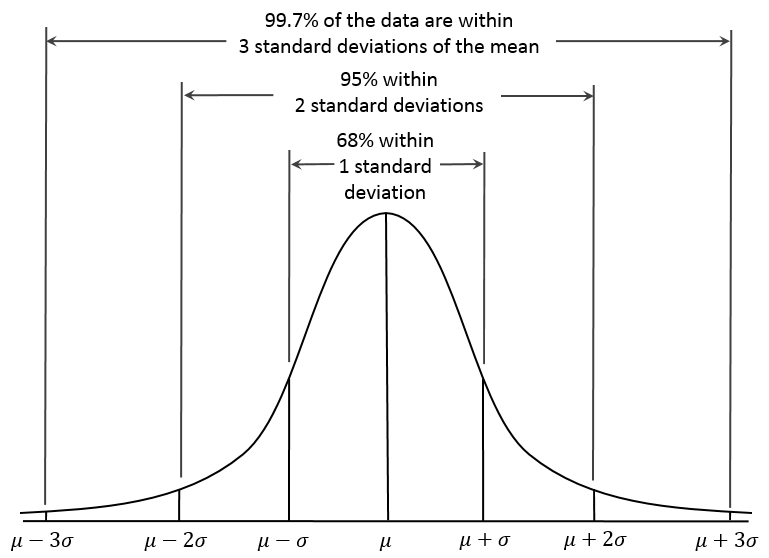
A contender would be the Normal Distribution curve, above, which encompasses so much of the natural and statistical world.

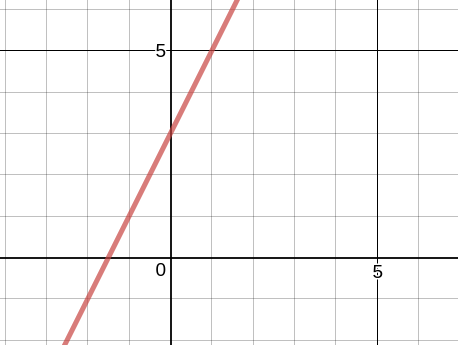
Or perhaps the more humble straight line: y = mx + c gets your vote

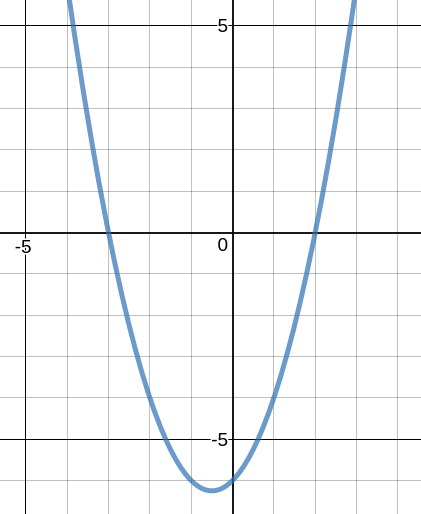
To simple? Well the quadratic curve crops up a lot and has the right level of difficulty to make it non-trivial, but is within the scope of all.

And then there is the sine curve, an understanding of which opens up a huge area of mathematics, not just a curve, but a wave.

But none of the above are my favourites, although they all stake a good claim.

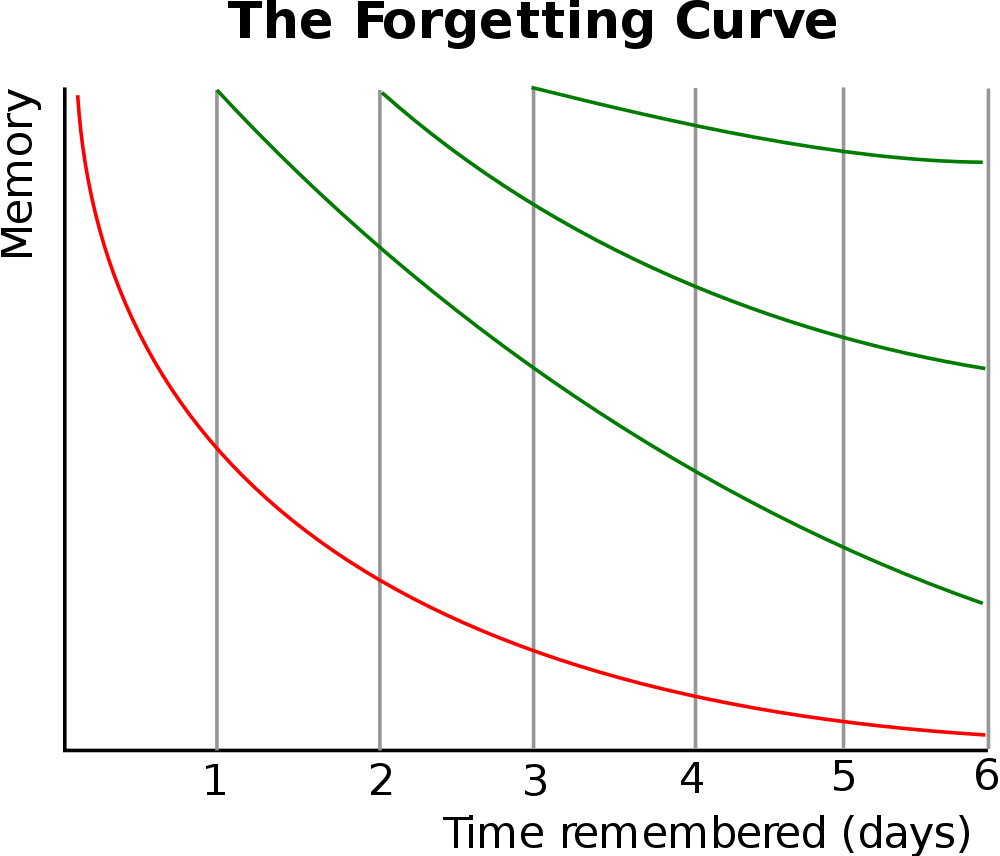
No, my favourite curve was first plotted by a somewhat obscure 19th Century German Physcologist, Hermann Ebbinghaus, his “Forgetting Curve”

I first came across his curve a few years ago, and it made instant sense to me. In essence, we quickly forget what we have learned, no matter how well we may have been taught. However, if we revisit the work we soon remember but once again, we soon forget, although the “speed” of our forgetting is diminished, and we don’t forget quite as much as we did before.

If we continue this process, each time we forget less and retain more.

It confirms what experience has taught me – that we need to constantly revisit and revise work, it is not enough to master a topic in a week, because in a month we’ll have forgotten most of it.

The idea is being given a modern spin (retrieval practice and spaced learning being a few new buzz words that use Ebbinghaus’ work) and, whilst I think I’ve always done this in my teaching, since discovering Ebbinghaus I’ve made a more conscious effort to resist the relentless pressure to plough on with the syllabus and revisit work covered earlier in the term and year.

For example, every few weeks we have unit tests – so we revise a few weeks work for the test (the first revisit), but then after the test I also devote a lesson or two to revisit unit tests from earlier in the year, thereby revisiting topics again and again as the year unfolds.

To find out more about the Ebbinghaus Forgetting curve, this Wikipedia page is a good starting point.

And, as an aside, I’ve often thought that investigating the Ebbinghaus Curve could make for a good EPQ project – plenty to research, plus the opportunity to devise one’s own test to try and replicate the curve, thereby creating primary data of their own.

(Now having read this blog post, make sure you came back next week, next month, next year … to ensure you don’t forget it!!)