
And so the sun sets on another Wimbledon tournament, one that will be remembered in part for the two losing singles finalists.
Serena Williams was the runner up in the ladies final, ten months after giving birth, and Kevin Anderson lost in the men’s final to Novak Djokovic, two days after playing the second-longest match in Wimbledon history, taking six hours, thirty six minutes to overcome John Isner in the semi-final.
Understandably, Anderson has called for a change in how close games are decided.
To win a tennis set, a player must win 6 games, and be two clear games ahead of their opponent. If the score is 6-6, the set is decided by a tie break, where the winner is the first to 7 points (as long as they lead by two clear points.)
Except for the final set of a match. If the fifth set is tied at 6-6, it continues – with no tie break – until one player leads by two games. And this is where the problem lies.
If both players are good and evenly matched (a reasonable expectation in the semi-final of a Grand Slam Tournament) then the maths tells us there will be a significant number of games before a player loses a game on their serve. i.e., stalemate sets in, with neither player able to break the opponents serve and win by the required two game margin.
The score in Friday’s final set was 26-24, i.e. it took fifty games to decide the final set.
Looking at the stats for the match, Anderson won 213 points from his 278 serves, giving him a probability of winning any point on his serve of 0.7661. Isner won 206 of his 291 serves, giving him a probability of 0.7071 of winning a point when he served.
To win game, you need to win (at least*) 4 points on your serve, with your opponent winning winning no, one or two points. We can use a bit of basic probability to work out the probability of winning “to love”, ” to 15″ and ” to 30″.
* The problem is made harder as we need to consider “deuce”, when the score reaches 40-40. Due to the need to win by two clear points, “deuce” games could go for ever. The good news is, is that we can model “deuce” games as a geometric series, which we can sum to infinity, thereby coming up with a probability for winning a “deuce” game.
Using the probabilities above, I was able to calculate the probability that each player would win a game when they were serving. More importantly, this allowed me to the calculate the probability they would lose a game on their serve, or have their serve broken.
To win the final set, the game would go on until (at least) a player lost a game on their serve, hence we could treat the game as a geometric distribution, meaning we could calculate the “Expectation” for games lost.
For Anderson, the expectation is 25, that means, you would expect him to lose one game for every twenty-five he plays. The number is a little lower for Isner: we would expect him to lose one game in every eleven.
What this means is is that we can expect long final sets, unless the pragmatic decision is made to revert to allowing tie-breaks in fifth and final sets. As players continue to improve, and the advantage of serve continues to increase, the sport’s administrators will have to grapple with this conundrum, or look forward to future marathons as the sport descends into a war of attrition.
If you are interested in the formula I derived to calculate the expectation, you can see it below. p is the probability of a player winning a point on their own serve.
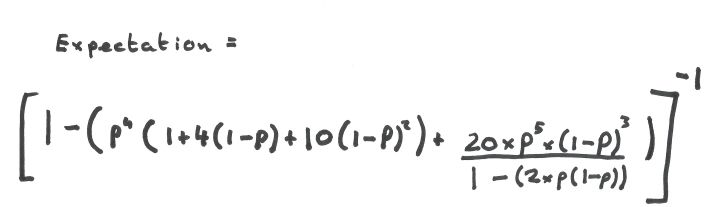
Expectation to lose a game on serve. p is the probability of winning a point on serve. The formula gives the average number of games in which one game would be lost (the others won) For example, Kevin Anderson has a probability of 0.7661 winning a point on his serve. The formula gives an expectation of 25 (rounded to the nearest whole number). This means we would expect him to lose one game in every twenty five he plays. (Note: it does not mean we would expect him to win the first twenty four then lose the twenty fifth, but in a series of twenty five games, he would lose one game.)
2 Comments